そういえばまだアレをやっていなかったな、と思いつく。
まだやっていなかったな、というのは正確ではない。やるのは30年ぶりくらいかな、というと正確だ。
アレ、というのは「マルチバイブレータ」という回路のことだ。
そう、この「マルチバイブレータ」という回路ををもとに少しづつカスタマイズを進めていくと「2安定マルチバイブレータ」、つまり「フリップフロップ」になり、それはそのまま1ビット記憶素子となり、やがてコンピュータそのものにつながっていくのである。
その原点の、「マルチバイブレータ」というのは下のような回路である。
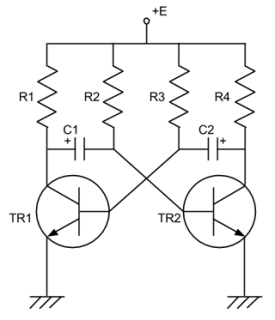
私などは若い頃、職場でこの回路を随分と叩き込まれたもので、当時は二つのトランジスタのところが真空管になっている回路がさまざまな機材の中にまだ現役で存在した。真空管でマルチバイブレータを構成する場合はヒータ回路などを一緒に考えなくてはならないことや、電圧が高いことなどで、実際に作動させるにはもう少し複雑な配慮が必要になる。その点、トランジスタで構成すると電力も少なくてすみ、単純明瞭だ。
回路自体の知財権等がどうなっているか、ということを今日まで知らなかったが、今ネットで少し検索してみると、Wikipediaには「イギリス人の物理学者ウィリアム・エックルスとフランク・ジョーダンによって1919年に作られた」とある。ウィリアム・エックルスは1966年に亡くなっているが、フランク・ジョーダンの没年は不明である。電子回路の知財権に関して、著作権はあいまいでよくわからないが、回路配置利用権については、日本では申請登録が必要で、かつ登録後10年となっている。要するにマルチバイブレータの回路図をネットでコピーしたり利用したりする場合の知財権関係の問題点は、回路配置利用権については申請されていないから存在しないが、著作権についてははっきりせず、よくわからないということである。しかし、マルチバイブレータの回路図は、あらゆる教科書に作成者の紹介もなく掲載されているので、多分ネットに書いても大丈夫なのではなかろうか。
さておき、この回路の動作原理は複雑で、理解するのは困難だが、動作結果や回路自体はご覧のように簡単なので、すぐに覚えてしまえる。すなわち、一方のトランジスタのベースをもう一方のトランジスタのコレクタにコンデンサをはさんで「たすき掛け」に接続し、それぞれの接続点に抵抗を全部で4つつなぎ、これを介して電源電圧を加え、最後にエミッタを接地する……、というふうに覚えるのだ。
発振周期の計算は私は恥ずかしながら覚えていない。しかし、ネットを漁ると、
……と、すぐにその式は出てくる。つまり、コンデンサふたつと、真ん中の抵抗ふたつで周期が決まる。両側の抵抗ふたつはトランジスタに流す電流を決めると思えばよい。この両側二つの抵抗をLEDの電流調整抵抗とみなせば、LEDはここに直列につなげばよい。
2秒に1回くらい、つまり0.5HzくらいでLEDをチカチカさせる場合を考える。とりあえず手持ちの部品で47μFの電解コンデンサがいくつかあるのでそれを使いたい。左右とも同じ周期で発振させるなら、この場合はR2とR3、C1とC2は同じ容量のものを使えばよい。なので、先ほどの式は
……というふうに簡単になる。
手持ちの電解コンデンサ47μFで、0.5HzくらいのLチカをやりたいときの抵抗は、
……というふうになる。
私のガラクタ箱の中に入っている一番近い値の抵抗は、10kΩだ。代わりにこれを使うと、結局、
……というわけで、2秒に3回くらいチカチカするものが作れる。
とりあえず、C1とC4、つまり両側の電流調整用には330ΩとLEDを直列に入れる。
適当なトランジスタがないので、買う。NPN型の定番品に2SC1815というのがあり、秋葉原千石電商で10個入りのパケットが150円だ。

この「2SC1815」は汎用的に使われている石なので、さまざまな電子工作にもよく登場している。余分に持っていて損はないし、10個で150円ならお金を使った気にすらならないので、一袋買っておくのは正解だと思う。
ブレッドボードに並べれば、次のようになる。

上のほうに3端子レギュレータを設け、ACアダプタの13Vを5Vに落としている。切り欠きのあるトランジスタふたつ、切り欠きに向かって左からエミッタ・コレクタ・ベースなので、――昔はこれを「E-C-B」とも「エ・ク・ボ」とも覚えたものであった――ベースから黄色いジャンパで「たすき掛け」になっているところがよくわかる。R1・R4が下のほうの抵抗で、茶・黒・橙(1・0・3、10×10の3乗)の10kΩであることが見て取れる。
動かすとこんな感じである。
次に、この「Lチカ周波数」をできるだけ正確に測ってみよう。私はオシロスコープなど持っていない。そこで、LEDの電流調整抵抗の後に直列にArduinoのデジタル入力をつなぎ、LOW~LOWの間をμ秒単位で計れば、周波数がわかるわけだ。電源も5Vなので、ちょうどよい。
スケッチをこのように書き……
// // MB2f.ino // 非安定マルチバイブレータの周波数を測る。 // 27.08.23(日) 1400~ // 佐藤俊夫 // #include <stdio.h> // const int MB = 2; // デジタル2番ピン // void setup() { pinMode(MB, INPUT); Serial.begin(9600); } void loop() { static unsigned long int prevtime = 0; static int prevstatus = HIGH; int nowstatus = digitalRead(MB); if(nowstatus != prevstatus){ if(nowstatus == LOW){ unsigned long int time = micros() - prevtime; float f = 1000000.0 / (time); char s[32], sf[32]; sprintf(s, "t = %ld microsec, f = %sHz", time, dtostrf(f, 5, 3, sf)); Serial.println(s); prevtime = micros(); } prevstatus = nowstatus; } }
それから、このように繋ぐ。

Arduinoのシリアルモニタで観測すると、波長から周波数が計算されてくる。
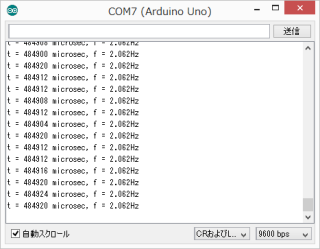
2.062Hzとなっているから、最初の計算の1.5Hzからすると、だいぶ誤差があるが、CR回路の発振なんて、こんなもんである。
さて、この「非安定マルチバイブレータ」は、回路にコンデンサが含まれていることにミソがある。ふたつのコンデンサが入っているからその充放電の働きにより発振し、放っておいても時間ごとに切り替わるのである。
そこでこのコンデンサをとっぱらい、少し回路の配置を変える。
そうするとアラ不思議、状態を保持する1ビットの記憶素子、「フリップフロップ」になるのである。
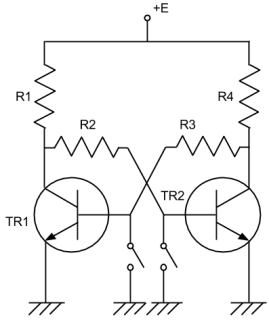
この場合、トランジスタのベースから出したスイッチを押すたび、状態が切り替わる。
ブレッドボードに組むとこうなる。

動かしている様子である。
ボタンを操作するたび、光っているLEDが代わる。二つの状態のいずれかを保持しているということであり、それが1ビットの記憶ということである。2安定マルチバイブレータが1ビットのメモリーだということがここからもわかる。

「そういえば、と」への1件のフィードバック