Raspberry Pi Zeroの続報がないなあ、などと思いついて、Amazonで検索したら、ビックリ……。
いっやー、
千円、ってならまだしも、1万円は、ないわ~。5ドルだろ、元の値段。今の円安でだってせいぜい650円だろー。
いくらなんでも、ナイわぁ~。ビックリして思わずレビューで星一つ付けてコキ下ろしてやった。
これ、一頃結構問題になった「Amazon詐欺」の
1000人に1人くらいいるアホを対象にしているということで、こういうのを「アホのロングテール」(下図)というわけですよ。
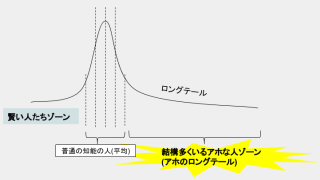
1000人に1人ぐらいしか引っ掛からなくても、このアホな人たちは結構多い。「ロングテール」の
くどく書くことではないが、ちょっと計算してみよう。仮に、Amazonで買い物をする人が単位時日に1000万人、そのうち1000分の1、1000人に1人の人がRaspberry Pi Zeroを買いたく思い、これらの人の中に一定の率でアホな人がおり、更にそのアホな人たちの中の20人に1人がコレに引っ掛かるとする。
「一定の率」と書いたが、上に掲げた「アホのロングテール」の図の、「結構多くいるアホな人ゾーン」というのを、「正規分布の2
片側2σよりアッチ、ということは、両側で4σということで、この両側4σの間には、圧倒的大多数、正規分布の場合は95.44%の人が含まれる。まあ、普通の常識人ですな。この95.44%に入らない人の中には、「突拍子もなく賢い人たち」と「信じられないくらいアホな人たち」が両方入っているので、それらを2で割ると、アホな人たちの率が出る。つまり、
となって、1000人につき23人はアホな人たち、つまり「騙され予備軍」である。このアホな人たちは割合に騙されやすいから、20人に1人くらいは引っ掛かるだろう、と仮定すれば、
11.4人。商材が1万円なら、これで11万円の売り上げだ。こんなアホな商材を10個も並べておけば、それで100万円だ。魚釣りみたいなもんで、アホの
数字は全部仮置き、つまり全部「仮に……」の話ではあるが、なんとなくそうだろうなあ、という気はするでしょ?
昔は、詐欺
こういうわけで、AmazonがEコマースのプラットフォームとしての地位を確立して以来、アホな人はロングテールでやって来るようになり、昔と違ってアホな人相手の商売ってのはそこそこ儲かるものに生まれ変わったのである。
そんなあれこれを見越してるわけだから、まあ、この会社ってのは、