プログラミング言語「R」というものを知る。
恥ずかしながら不肖この佐藤、これまで数多くのプログラミング言語を扱ってきたし、10種やそこらはゆうに越える種類のプログラミング言語で実用にかなうプログラムを書き、実際に使用もしてきた。また自らプログラミングしたことがないいろいろな種類の言語でも、その名前や特性、出所来歴は知っている。…つもりでいた。
迂闊であった。
この「R」という言語など、まったく全然、少しもちっとも、知らなかった。知ったのは一昨日である。
なぜ知ったのかというと、マルコフ決定について学ばなければならず、それにはマルコフ連鎖をわきまえなければならない。マルコフ連鎖について書かれたサイトを渉猟していると、「ここをRで説明すると…」などとして説明しているサイトに行き当たった。ナニ、Rで説明だと!?Rて何だ?知らん。聞いたことがない。
さてそういうわけで、さっそくRのバイナリをダウンロードしてインストールし、試す。オープンソースにしてフリーであり、お金はかからない。Linux/Windows/Macと、色々な種類の計算機で動く。Windows用バイナリは次のURLにある。
Rは統計解析に向く言語で、Rという言語仕様そのものよりも、そのインタプリタ風実行環境――かつてのBASICに似ている――全体を含めて、統計処理がしやすく作られている。コンソールにコマンドを打ち込んでいくだけですぐに結果が得られる。電卓代わりに使うだけでもなかなか便利だ。
ふと思いついて、このRと、「ランチェスターの2次則」で土曜日の昼下がりを遊んでみようか、という気になる。
ランチェスターの2次則は、オペレーションズ・リサーチの古典理論として知られている。もともとはイギリスの技術者ランチェスターが、まだ飛行機が戦力として有望でない第一次大戦の時代に、将来飛行機が大量に使用されるときの損耗の推移を考察・研究し、発表した軍事理論である。
歴史上のさまざまな戦争の戦闘経過をこの公式にあてはめると、まるで嘘じゃないかというほどよく合致するので、オペレーションズ・リサーチの分野でよく知られ、いまなお良く使用されている。日本では企業の競争などのモデルに使われており、これが実は軍事理論であるとは知らない人も多い。
式は実に簡単だ。
ここに、
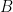
: 青軍
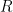 : 赤軍
: 赤軍
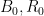 : 青・赤両軍の最初の兵力
: 青・赤両軍の最初の兵力
 : ある同じ時点での青・赤両軍の残存兵力
: ある同じ時点での青・赤両軍の残存兵力
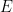 : 兵力の質の比。赤軍の質が青の倍であれば2、半分であれば0.5。
: 兵力の質の比。赤軍の質が青の倍であれば2、半分であれば0.5。
まことに単純きわまる。何の疑問もない式だ。「E」が1.0のとき、それぞれ全く同じ人数の青、赤両軍が全員で殺し合いをすれば、双方とも等しく損耗し、同時に全滅する。しかし、兵力に差があると、その差に「自乗」が作用し、思っているよりも損耗差が大きく開いていく、という式だ。
ここで「だから戦争はしてはいかんのだ」と脱線するのもなかなか楽しそうだが、今日は脱線しない(笑)。
式を変形すると、例えば、
などという、まことに楽しげな式ができる。ここで、赤軍(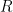 )が劣軍として、
)が劣軍として、 にゼロを代入し、
にゼロを代入し、 、
、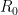 に開戦時の兵力を入れれば、赤軍が全滅したときに青軍がどれくらい残っているか、ということを見積もることができるのである。また、
に開戦時の兵力を入れれば、赤軍が全滅したときに青軍がどれくらい残っているか、ということを見積もることができるのである。また、
とすると、例えば兵力が足りない側が、どれくらい優れた兵器を持たなければならないか、ということも簡単に見積ることができる。
ランチェスターの2次則はほかにもいろいろとイジりがいのある理論で、たとえば「 」に関する最初の変形を微分して導関数を出せば、某時点での接線の傾きが求められるから、「傾き1以上」になるときの兵力がいくつか、ということから、「急に敗色が濃厚になってきたのがいつごろか」などというものも計算でき、これがまた、歴史上の色々な戦例に合致したりするから侮れない。
」に関する最初の変形を微分して導関数を出せば、某時点での接線の傾きが求められるから、「傾き1以上」になるときの兵力がいくつか、ということから、「急に敗色が濃厚になってきたのがいつごろか」などというものも計算でき、これがまた、歴史上の色々な戦例に合致したりするから侮れない。
さて、起動したRのコンソールに、次のように入力する。
> # 関数Bt
> Bt<-function(B0,R0,Rt,E){
+ Bt=sqrt(B0^2-E*(R0^2-Rt^2))
+ Bt
+ }
これで、ひとつ目の変形、「双方の初期兵力と、赤軍の現在兵力及び双方の兵力の質に応ずる青軍の現在勢力」を求める関数が定義される。
この関数で、実際の勢力の推移を求めよう。Rでは、こんなふうにすると、たちどころに数列が配列に格納される。
> Bts<-Bt(100, 80, 80:0, 1.0)
これで、劣軍勢力が80から0になるまでの、優軍勢力の推移が配列Btsに格納される。格納された様子を見るには、配列名をタイプするだけでいい。
> Bts
[1] 100.00000 99.20181 98.40732 97.61660 96.82975 96.04686 95.26804 94.49339
[9] 93.72300 92.95698 92.19544 91.43850 90.68627 89.93887 89.19641 88.45903
[17] 87.72685 87.00000 86.27862 85.56284 84.85281 84.14868 83.45058 82.75869
[25] 82.07314 81.39410 80.72174 80.05623 79.39773 78.74643 78.10250 77.46612
[33] 76.83749 76.21680 75.60423 75.00000 74.40430 73.81734 73.23933 72.67049
[41] 72.11103 71.56116 71.02112 70.49113 69.97142 69.46222 68.96376 68.47627
[49] 68.00000 67.53518 67.08204 66.64083 66.21178 65.79514 65.39113 65.00000
[57] 64.62198 64.25730 63.90618 63.56886 63.24555 62.93648 62.64184 62.36185
[65] 62.09670 61.84658 61.61169 61.39218 61.18823 61.00000 60.82763 60.67125
[73] 60.53098 60.40695 60.29925 60.20797 60.13319 60.07495 60.03332 60.00833
[81] 60.00000
さて、数字の並びを見てもつまらないから、これをグラフにしてみたい。グラフを描くのも、Rでは簡単だ。
> # プロット
> plot(Bt(100, 80, 80:0, 1.0), 80:0, "l", xlim=c(100, 60))
Btsに値が格納されているなら、
> plot(Bts, 80:0, "l", xlim=c(100, 60))
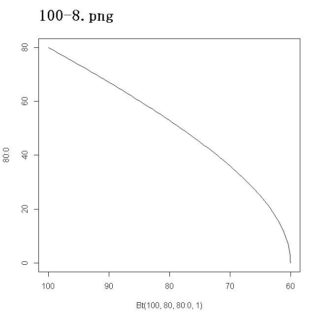 でよい。そうすると、画像のようなグラフがたちどころに表示される。
でよい。そうすると、画像のようなグラフがたちどころに表示される。
これは、80人対100人で戦って、劣軍(80人)側が全滅したときに優軍(100人)側が何人残るか、というグラフである。「自乗」がよくきき、最初互角に戦っているように見えて、ある時点から急速に80人側が損耗し、80人側が全滅したとき、100人側には60人もの残存兵力があることがわかる。
そうすると、劣軍のほうは、「量より質」で勝負、ということになるから、先に出た「E」を、互角の損耗になるように求めればよい。Rでは次の如しである。
> # 函数E
> E<-function(B0, Bt, R0, Rt){
+ E<-(B0^2 - Bt^2)/(R0^2 - Rt^2)
+ E
+ }
> E(100, 0, 80, 0)
[1] 1.5625
最後に出ている、「1.5625」、約1.6というのが、劣軍が持たなければならない「質」である。なんでもよい、命中率が1.6倍でも、飛行機のスピードが1.6倍でもよい。しかし、「モノの性能や人の能力が1.6倍」ということがどんなに難しいことか、論じるまでもない。オリンピックのスキー・ジャンプの選手が、相手が100メートル飛ぶところを160メートル飛ぶなどと、そんな途方もない実力差など到底保ち得ないことからも、それはイメージできる。
ここで、ちょっと、英雄・東郷平八郎元帥を揶揄してみよう。
日本海海戦にみごとな勝利をおさめた元帥が、戦後聯合艦隊を解散するに当たり、部下幕僚の秋山真之をして起案せしめた名文に、「聯合艦隊解散之辞」がある。その中の一節は不朽の名文として後世に残る。
(前略)
而して武力なるものは艦船兵器等のみにあらずして、之を活用する無形の実力にあり。百発百中の一砲能く百発一中の敵砲百門に対抗し得るを覚らば、我等軍人は主として武力を形而上に求めざるべからず。
(後略)
さて、では、100対1の勝負、そして100門側の命中率は100発中1発命中、すなわち0.01、かたやは100発中100発命中、というからにはすなわちこれは1.0であり、その性能比は100になんなんとする。
では、これを、Rを使って確かめてみよう。100対1だとグラフにしにくいから、1000対10にする。
> Bts<-Bt(1000, 10, 10:0, 100.0)
> Bts
[1] 1000.0000 999.0495 998.1984 997.4467 996.7949 996.2429 995.7911 995.4396
[9] 995.1884 995.0377 994.9874
…あっれ~…。どうも、ヘンだぞ、この数字は(笑)。グラフにしてみよう。
> plot(Bts, 10:0, "l", xlim=c(1000, 994))
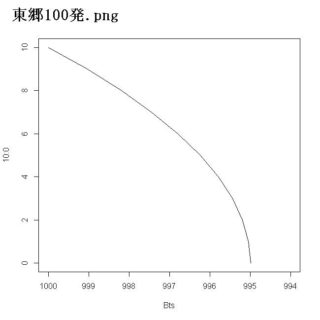 ……ダメじゃん。全然。東郷さん、相手を5門もやっつけないうちに、10門、全滅してんじゃん。秒殺じゃん。っていうか、これ、瞬殺のレベルでしょ。
……ダメじゃん。全然。東郷さん、相手を5門もやっつけないうちに、10門、全滅してんじゃん。秒殺じゃん。っていうか、これ、瞬殺のレベルでしょ。
秋山真之~ッ!!ウソ書くな~ッ(笑)。
じゃあ、なんで、日本海海戦に、弱い日本が勝てたの?どうしてどうして!?
……これは皆さん、実は日本海軍は当時劣勢海軍などではなかったのだ。ユダヤ商人からなりふりかまわず借金しまくり、戦闘艦艇を買いあさり、乾坤一擲の大勢力を作り上げていたのだ。これらはあげて一丸となってバルチック艦隊に襲いかかっている。
数において劣り、かつアフリカ回り、インド洋、南洋回り航路を遠路はるばるやってきて、疲弊しきっているバルチック艦隊を容赦なく待ち伏せ、さながら弱い者イジメのように袋叩きにしたという歴史的事実は知る人ぞ知るところである。そして、日本がそのためにした借金を返し終わるのに、実に82年後の昭和61年(1986)までかかっているのも、よく知られている。
「『数において劣る』だって!?いや、たしか、艦艇の数は互角だったんじゃなかったっけ?」
……と、詳しい向きは言うかもしれない。だが、双方の主要な火力であった15サンチ砲の門数だけを見ると、聯合艦隊204門に対してバルチック艦隊152門で、聯合艦隊が優るのだ。これをRに入れてみると、
> Bts<-Bt(204, 152, 152:0, 1.0)
> Bts
[1] 204.0000 203.2560 202.5142 201.7746 201.0373 200.3023 199.5695 198.8391
~中略~
[153] 136.0588
> plot(Bts, 152:0, "l", xlim=c(200, 133))
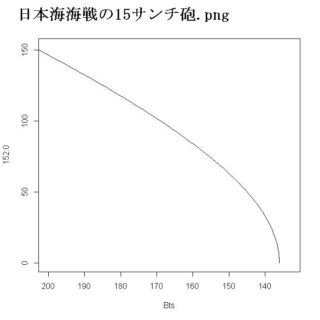 バルチック艦隊全滅時点で、聯合艦隊はまだ半分以上、136門の火力が残存しているのである。聯合艦隊の全艦艇は91隻、平均すると一隻につき2門の15サンチ砲を積んでいたことになるから、その片砲を失っていても、まだ船自体は沈まない。だから東郷平八郎が、「数に劣る日本軍は、腕前と作戦で勝った」と言っているのは、ウソなのである。数で押しまくり、バルチック艦隊を袋叩きにしただけだ。
バルチック艦隊全滅時点で、聯合艦隊はまだ半分以上、136門の火力が残存しているのである。聯合艦隊の全艦艇は91隻、平均すると一隻につき2門の15サンチ砲を積んでいたことになるから、その片砲を失っていても、まだ船自体は沈まない。だから東郷平八郎が、「数に劣る日本軍は、腕前と作戦で勝った」と言っているのは、ウソなのである。数で押しまくり、バルチック艦隊を袋叩きにしただけだ。
さておき、この「東郷平八郎・ランチェスター検証ネタ」は、私・佐藤のオリジナル着目ではない。オペレーションズ・リサーチの専門家の間ではよくネタとして取り上げられるものであることを断っておく。また、恐ろしい戦争で、恐怖に耐えて一生懸命に戦った下士官兵たちを、「よくやった!お前たちの精神力がまさっていたから、勝った!!だが油断するなよ!」と、提督として元気付けている類の話を、数字の計算だけを論拠にウソだなどと言い立てることは、必ずしも正しいことではないと、漏れなく付言しておきたい。
さて、ここまでならExcelなどでも簡単にできることだ。ひとつ、Excelではちょっと難しい量の数字を、この面白そうな「R」言語に、叩き込んでみようではないか。
お題:「13億4千万の中国人と、1億3千万の日本人が全員で殺し合いをする」
…いや、これ、計算する前から結果は見えてるんですけど(笑)、そうじゃなくて、まあ、デケぇ数字でもRは扱えまっせ、というところを試したいのである。 このお題、エクセルで兵力の推移などを表で見ようとすると、人口が多すぎて、行数が足りなくなったりするからだ。
> Bts<-Bt(1340000000, 130000000, 130000000:0, 1.0)
エラー: サイズ 991.8 Mb のベクトルを割り当てることができません
…ありゃ(笑)。さすがに13億とか1億3千万とか配列に入れると、チトムリだったみたいだ。一桁減らそう。
> Bts<-Bt(134000000, 13000000, 13000000:0, 1.0)
サクッと配列に表が格納される。プロットしてみよう。
> plot(Bts, 13000000:0, "l", xlim=c(134000000, 133300000))
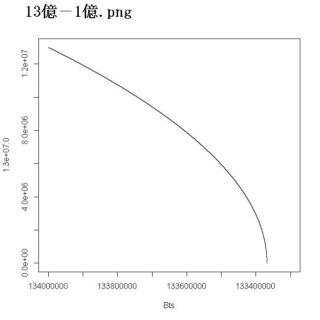
中国側が13億4千万から、13億3千万にまで減らない間に、日本はゼロ人。1億3千万人が全滅である。
では、ハイテク兵器などで武装して、量より質でがんばりましょう、としたとき、日本はどれほどの命中率、どれほどのスピード、どれほどの爆発力、どれほどの優れた人材を備えて、はじめて互角になるでしょうか、という数字が…
> E(1340000000, 0, 130000000, 0)
[1] 106.2485
…となる。106倍。
そんな、アンタね(笑)。中国の兵隊の知能指数が日本の100分の1であるとか、日本の飛行機が中国の飛行機の100倍のスピードで飛ぶとか、そんなのムリに決まってる。中国軍の100倍の厳しい訓練を自衛隊がしたって、100倍の能力にはならないのだ。
さて、これが今日の昼下がりの、「R」を使った、ちょっとした暗いお遊びでございました。どっとはらい。



