オッサンは生きている。
第1次大戦当時のオスマン帝国は、ドイツと同盟を結び、ガリポリでは名将ムスタファ・ケマル・アタテュルク元帥が頑強な防御戦闘を行って英国をはじめとする協商連合軍を撃退するなど善戦した。
しかし、有名なロレンス大佐の秘密工作によるアラブの反乱や、コーカサス山脈での敗走などもあり、 次第に劣勢となり、民心も政府も疲弊し、皇帝メフメト6世はついに降伏の詔勅を発した。
オスマン帝国は領土を蚕食され、協商連合の進駐軍がイスタンブールに蟠据、しかも西からはギリシャ軍が新たな戦端を開いて侵攻してきた。
ところが、その頃パレスチナ戦線で戦っていたムスタファ・ケマルはこれを聞いて “妄想・大東亜戦争後” の続きを読む
今日は話題の映画「アルキメデスの大戦」を観に行った。
劇中で、主人公が映画の核心ともなる数式を得るシーンがある。近似式で、軍艦を建造するために必要な鉄の単位量あたりの経費を数理モデルにあてはめたものだ。
映画のストーリーはさっさと進むので、主人公が素早く黒板に書き出す数式をいちいち見ている暇はなく、細部はよくわからなかった。だが、主人公が紙や黒板にグラフを描き出すシーンがあり、ふとそれに注意を惹かれた。
そのグラフは「ある一定のところまでは鉄の単位量当たりの経費は増えていくが、ある一定量を超えると工作が単純となるため、単位量当たりの経費が漸減していく」というものだ。映画では一瞬だけ画面に出る。
これが、IT技術者が古典的な工数モデルとして慣れ親しんだ「Putnam(パトナム)モデル」と非常によく似ていた。
Putnamモデルというのは次のようなものだ。
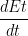
が最大となる時刻tこのモデルをグラフにとると次のようになる。
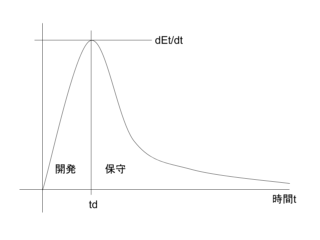
このPutnamモデルを積分すると、「S字成長曲線」に似ることもよく知られるところだ。逆に言うと、S字モデルを微分するとPutnamモデルに似た曲線になるのである。
工数はそのまま金額に比例するから、映画のシーンを見ていて「おっ、これは」と感じた。
帰宅してから、映画のサイトや他の方のレビュー記事などを見ると、主人公が黒板に書き出す数式は実数の定数の他は1個の説明変数があるだけのシンプルなもので、自然対数が現れる「レイリー分布曲線」を使用したPutnamモデルとは違うことがわかり、ちょっと肩透かしを喰った気になった。
なんにせよ面白い映画で、いろいろと考えさせられるところ大であった。