某時某所にて……
友達 「富士山から見たら、どこまで見えるかなあ」
私 「さあ？……結構遠くまで見えるんじゃねえの？」
友達 「太平洋の島とか見えるかな？」
……と、たわいない雑談である。
私 「さあ～？……どこまで見えるかは知らんが、苦労して登頂すれば、浄土とか天国とか、あるいは『希望』『幸福』といったような、形而上のブツがホノ見えるんじゃないか？」
とまあ、これは雑談であるから、どこまで見えるなんて答えは実際なんだってよく、どうでもよいわけである。
しかし、計算せよとなれば、これは簡単なようでいて、その実、掘り下げるといろいろあって深い。
簡単に図示すると、こういうことだ。
富士山から見たら水平線はどれくらい遠くにありますか、という図だ。雑談の「どこまで見えるか」、ということになると、見る対象物にも高さがあるのでこの図の通りではなくなってくるが、とりあえずこうしておこう。
もうちょっと算数っぽく、幾何っぽく描くと、こういうふうになる。
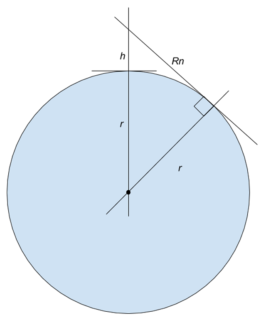
このように図示してしまえば、まことに単純きわまる。これは、学校で習う「ピタゴラスの定理」の問題だ。
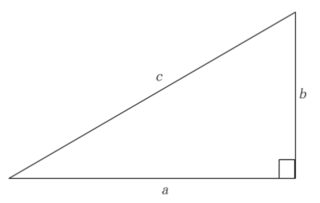
定理を問題にあてはめると、
ここに
r: 地球半径
h: 富士山の高さ
Rn: 水平線までの距離
と、いうわけであるから、実際の数字を調べ、関数電卓でポチポチッと計算すればよい。
地球の半径、図中の「r」はだいたい6千4百キロメートルくらいと言われている。富士山の高さは3776メートル。
私 「ほほぉ、だいたい220kmぐらいまで見えるみたいだぞ」
友達 「佐藤よぉ、だからお前はツメが甘いってんだよ。お前さ、富士山は『3776メートル』ってメートル単位で足しときながら、地球はザックリ6千4百キロメートルって、100キロ単位じゃねえか。そりゃねェだろ」
私 「ぬぅ……しからば、ネットでチョイと検索したら出てきた、この『6千371キロ』ってのを使おうじゃないか」
私 「これでどうだ。だいたい220キロっ！！結局数字はあんまし変わらんだろ？？」
友達 「いや、変わる変わらんじゃなくて、姿勢の問題だろうが。それに佐藤、地球は楕円体なんだぜ？赤道半径と極半径は違うワケだからさ～」
私 「細かいやっちゃのぉ～……。ああ、もう、はいはい、えーっと、ググると地球の扁平率はだいたい300分の1、と出てるから、さっきの6371キロを300で割って、それを6371から引きゃあよい、と」
私 「んでもって、本当に楕円でやると、経緯度によって複雑に水平線の形が変化して、水平線までの距離はいくら、という計算は簡単には出なくなるから、ここは平均してしまおう」
私 「で、計算をやりなおすと……」
私 「これでどうだ？」
友達 「あー、ダメだな」
私 「何でだ？」
友達 「だって佐藤よ、地球の楕円体は研究機関や国によっていろいろあるだろうが、世界測地系とか日本測地系とか」
私 「……だーっ！ウルサイウルサイっ！やれば文句ないんでしょうが、やれば！！」
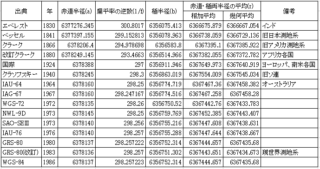(データはコチラ) ここでは各種出典の楕円体を挙げた。
友達 「ほぉ～……調べたねえ」
私 「ゼイ、ゼイ……。調べたぞっ。……で、このGRS-80かWGS-84あたりを使っとけば文句ないだろっ？んで、幾何平均を使っとこうじゃないの！」
私 「どうじゃっ！！だいたい220キロっ！！……って、最初から全然数字変わってないけど！！」
友達 「佐藤、お前さ、これ、『真空の場合』じゃん。『光』ってものはさ、地球大気の密度差で
私 「お前、ほんっと細かいな。そんなネチネチしていて、よく今まで何事もなく生きてこれたと思うよ！！……へいへい、『等価地球半径』ね」
そう。電波や光は回折する。その回折曲線を加味して計算するのは多少骨折りなので、実用上は扱う波長に合わせて地球の半径をちょっぴり大きくしてやるわけだ。これを「等価地球半径」と言う。
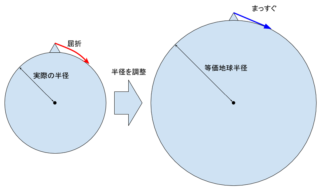
この等価地球半径、電波の場合は地球半径の
私 「じゃ、やりますよ。やりゃいいんでしょ。……世界測地系の平均地球半径6367435.68に等価地球半径係数をかけまして……」
私 「んで、これと富士山の標高使って……」
私 「……って、だいたい237キロ。……おお、数字がちょっと変わったぞ。14キロぐらい多く見えるな。わっはっは、大気様々よのう！Google Mapで237キロを測ってみると……」
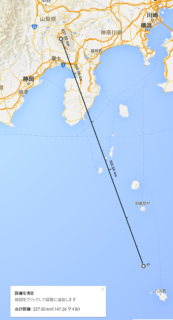
私 「おお、八丈島はちょっとムリだが、理論上は御蔵島辺りまでは見えるっちゅうことになるな」
友達 「佐藤よォ。いいんだけどさ、地球の楕円体なんて仮決めのもので、実際はゴツゴツした岩石がいろんな密度で分布してて、つまりこれが『ジオイド』ってやつだ、海面ですら幾何学的な楕円体なんかじゃないんだぜ？だから、お前の計算はナンセンスだ。全部意味がない」
私 「殺すぞキサマ(笑)」
