バーニヤは素晴らしい。何が素晴らしいかと言うと……
昨日、「バーニヤというのを考えた人は偉い」みたいな事をメモしておいた。
当然、この原理を考えたフランス人数学者・バーニヤ氏は偉い。
だが、バーニヤ目盛りの原理以前に、それを実際に制作するのには非常に難しい関門がある。実製作上最も困難なその部分を
「1センチ幅の目盛りがある。これを9等分した目盛りを作れ。」
……ということだと、私は思う(下図)。
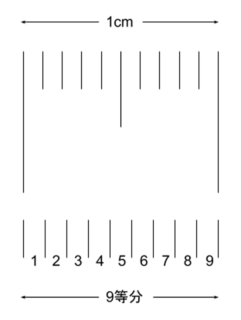
紙と鉛筆、定規程度の簡素なものでやる、という前提だ。精度の高い0.1ミリ定規とか、そういうすごいものは、この場にはない。パソコンの使用もだめだ。
もし、これをお読みの方がいらっしゃったら、読み進める前に、「自分だったらこうする」と考えていただくと面白いと思う。考え付くだろうか。
もし、普通の人がこれをやることになったら、多分、
「そんなの簡単だよ!1センチは10ミリだろ?10ミリを9で割れば、1.1111……ミリだろ、四捨五入して、1.1ミリごとに目盛りをふればそれでおしまいじゃないか!?」
……と言うと思う。
うーん。それでもいいんですがね……。だけど、1.1ミリ毎に目盛りをふると、9個目の目盛りで0.01111……×9≒0.09≒0.1ミリの誤差が出る。一見些細な誤差に思えるが、1.1ミリごとにふっている目盛りで、10%もの誤差は大きすぎる。
私は若い頃、仕事の上で、これを作図で正確に行うテクニックを覚えた。電子計算機パワーがあまり使えない職場で、精密作図で数値解を求めるような仕事をしていたのだ。測定するための機材・資材の目盛りが温度や湿度で伸縮し、精密さが損なわれた環境下で、できるだけ正確に数値解を求める際に使用した方法だ。
誰が考えた方法かは知らない。が、恐らく昔、定規製造の職人などが使用していた方法なのではないかと思う。昔の定規の素材は木や竹、品質にばらつきのある樹脂などで作られていたからだ。
以下、その方法を説明したい。なぜ説明したいかと言うと、これはいろいろな場面で非常に役立つからだ。
1センチ幅を9等分する方法
1 できるだけ正確に、1センチ幅の平行線を引く。
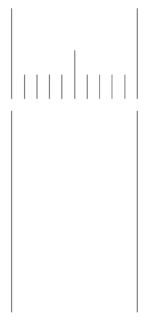
2 引いた平行線に、定規を斜めに当てる。この際、9ミリの倍、18ミリになるように当てる。
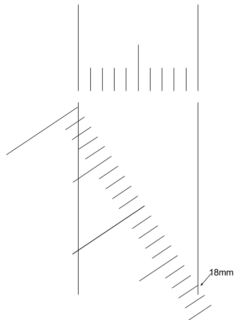
3 定規で2ミリ毎、正確にに印をつける。
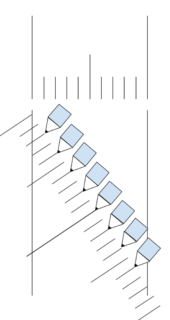
4 つけた印に従い、並行に線を引いていく。平行線を引くには、三角定規などを定規と併用すればよい。
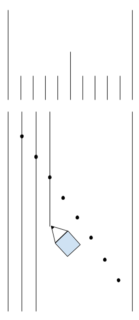
5 アラ不思議、1センチが9等分された、1.1111111……ミリごとの目盛りができる。
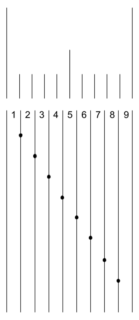
こうして、作図によって、割り切れない循環小数になるような区間にも「アナログに」目盛りをふることができる。
参考までに、実際のノギスの

写真のノギスの場合は39ミリを10等分した
前述の説明と同じように、「39ミリ幅の平行線を作り、定規を40ミリになるように斜めに当てる。4ミリごとに目盛りをふれば、10等分できる」わけである。
この方法の応用
「1センチ」を例に挙げたが、原理から言って、別に1センチでも、測らずにえいやっ!と引いた何センチ間隔かわからない平行線の間でも、また9等分だけでなく、13等分、11等分、7等分、3等分など、「素数分の1」系の、どんなヤヤコシイ等分目盛りも作ることができる。また、工夫すれば、「並行でない線」の間を精密に等分することも可能である。
私は以前、同じ方法の応用で次のようなことをした。印刷物に掲載されたグラフからデータを高精度で読み取る必要に迫られたのだが、この印刷物の方眼目盛りは歪みこそなかったものの、不定縮尺、すなわち、センチ単位やミリ単位でふられておらず、また縦横の比率に伸縮があった。その時、上記に説明した方法を応用し、精密定規を斜めにグラフに当てて読み取った。
また、斜めに撮影された不鮮明な写真のグラフなどから数値を読み取るようなことも、この方法を応用して工夫すればできる。
私は仕事上の理由でこれを覚えたが、この方法には多分、「なになに法」というような名前があるのだろうと思う。だが、名前はわからない。
言うまでもないことだが、今はIT万能の時代だ。上記のような応用例なら、今は例えばスキャナで読み取って、ピクセル毎の寸法を出すなりすれば、相当高精度で同じことができるだろう。ここで紹介したのは古い古いやりかただ。
それを解っていて、